Teorema Del Valor Medio Del Calculo Diferencial Ejemplos

Colección de administrador en Teorema Del Valor Medio Del Calculo Diferencial Ejemplos.

Cómo aplicar el teorema del valor medio. Hallar el valor medio en el intervalo 14 y obtener el valor del punto para el cual se verifica dicho valor de la siguiente función.

El Teorema Del Valor Medio Y Sus Aplicaciones Ejercicios

Ejemplo Del Teorema Del Valor Intermedio Una Función Radical Cálculo Khan Academy En Español

Teorema Del Valor Medio De Una Función A Trozos

Teorema Fundamental Del Calculo Decifra El Significado Del

Teorema Del Valor Intermedio Wikipedia La Enciclopedia Libre

Teorema De Valor Intermedio Aprende Matemáticas

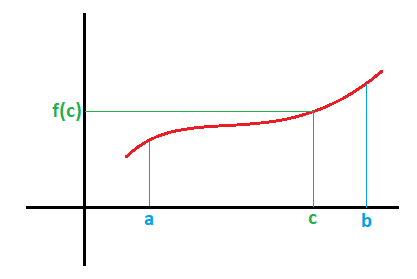
Geométricamente el teorema del valor medio establece que dada una función positiva en a b el área del recinto limitado por la gráfica de la función el eje ox y las rectas x a y x b coincide con el área de un rectángulo de base igual a la longitud del intervalo b a y altura fc siendo c un punto del intervalo a b.

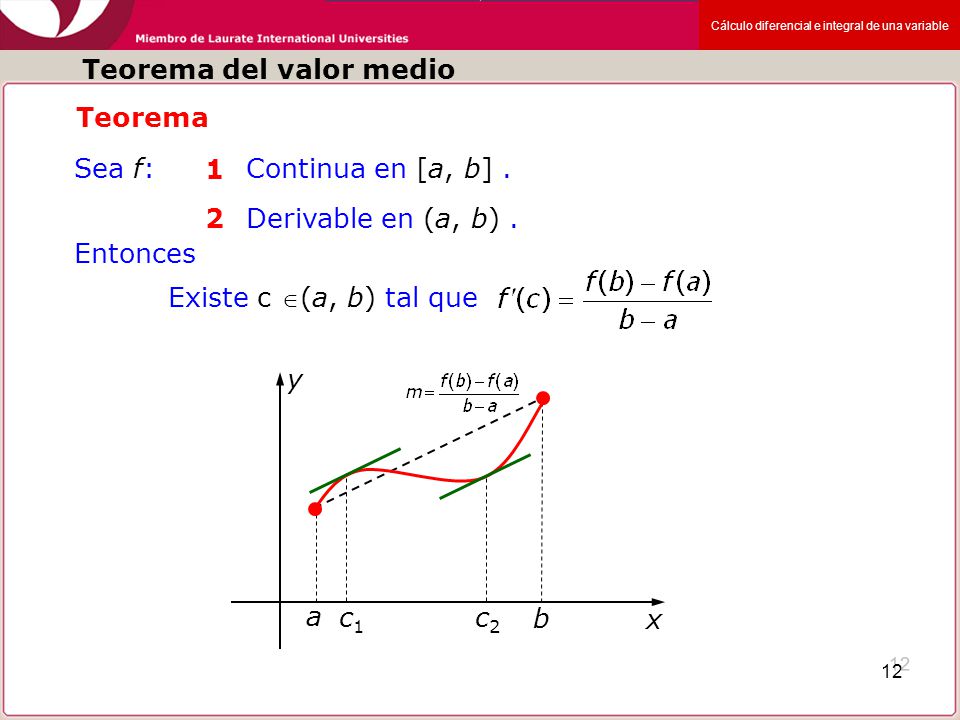
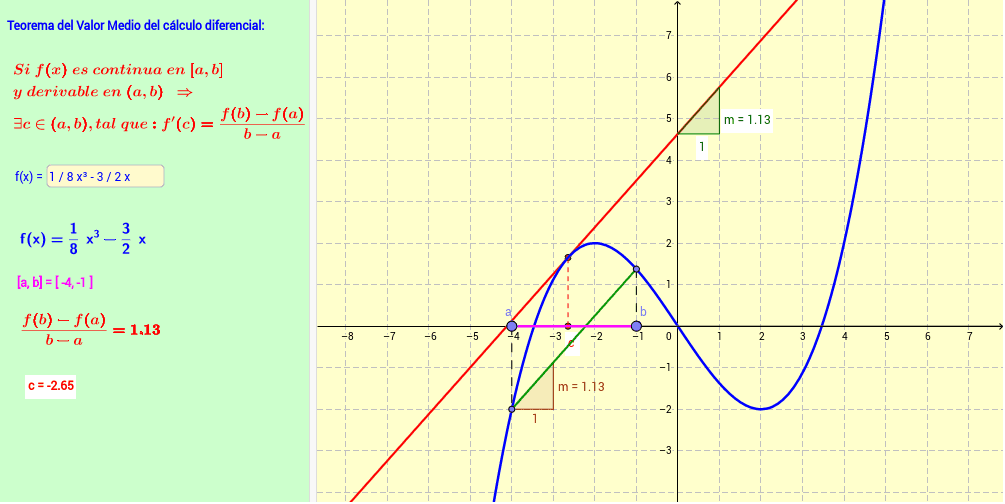
Teorema del valor medio del calculo diferencial ejemplos. Problemas y ejercicios resueltos del teorema de valor medio o teorema de lagrange o teorema de los incrementos finitos y teorema de cauchy. Por ser la función polinómica se puede aplicar el teorema del valor medio en el intervalo 1 3. En este vídeo demuestro el teorema del valor medio para la integral y hago un ejemplo que compruebo utilizando geogebra. Qué teorema garantiza la existencia de dicho punto. Vamos a ver ahora algunos ejemplos de cómo aplicar el teorema del valor medio y calcular el punto c del teorema. Calcular un punto del intervalo 1 3 en el que la tangente a la curva y x 3 x 2 2 sea paralela a la recta determinada por los puntos a1 2 y b3 20. En la figura de la izquierda se ilustra este hecho. En cálculo diferencial el teorema de valor medio de lagrange teorema de los incrementos finitos teorema de bonnet lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Esta se refiere al punto iii f a f b. La interpretación geométrica del t eorema de lagrange nos dice que si la gráfica de una función continua tiene tangente en todo punto del arco ab entonces hay por lo menos un punto c en el que la tangente es paralela a la. Por ser la función polinómica se puede aplicar el teorema del valor medio en el intervalo 1 3. Ejercicios resueltos del teorema del valor medio. Teorema del valor medio del cálculo diferencial expresión que recibe el nombre de fórmula de incrementos finitos.

Aplicación del teorema de lagrange para el cálculo de la recta tangente dados sus extremos. Vamos a ver cómo aplicar la fórmula del teorema del valor medio del cálculo integral con un ejercicio resuelto paso a paso. Algunos matemáticos consideran que este teorema es el más importante del cálculo ver también el teorema fundamental del cálculo integral. 10 calcular un punto del intervalo 1 3 en el que la tangente a la curva y x³ x² 2 sea paralela a la recta determinada por los puntos a1 2 y b3 20. éste vídeo es complemento para el ví. Basta con que el valor de la función sea el mismo para x a y x b y no necesariamente sean iguales a cero. Comprobación de las hipótesis del teorema de lagrange y cálcuo del punto medio dada una función y un intervalo. El teorema de rolle es susceptible de una modificación en su enunciado que no altera para nada la conclusión del mismo. Calcula el punto c que satisface el teorema del valor medio para la siguiente función en el intervalo 01.

Información detallada sobre teorema del valor medio del calculo diferencial ejemplos podemos compartir. Administrador Opciones de Ejemplo blog 2019 también recopila imágenes relacionadas con teorema del valor medio del calculo diferencial ejemplos se detalla a continuación.

Taller 11 Cálculo Diferencial Clases 25 27

Problemas De Optimización Teoremas Rolle Valor Medio L

Problemas Y Ejercicios Resueltos Del Teorema De Valor Medio

Teorema Del Valor Medio Del Cálculo Integral Ejemplos Resueltos

Ejercicios Del Teorema De Rolle Y Del Valor Medio Superprof

Teorema Del Valor Intermedio Docsity

Teorema De Rolle Teorema De Lagrange O Teorema Del Valor

Teorema Del Valor Medio Del Cálculo Integral Ejercicios

Teorema Del Valor Medio

Teorema De Rolle Y Teorema Del Valor Medio

Teorema Del Valor Medio Ppt Descargar

Cómo Aplicar El Teorema Del Valor Medio A Una Función Integral

Clase 13 Parte 1 Funciones Reales De Dos Variables Plano

Teorema Del Valor Medio Lagrange Geogebra

Reconocimiento Fisiográfico 1

Del mismo modo la información completa sobre teorema del valor medio del calculo diferencial ejemplos. Gracias por visitar el blog Opciones de Ejemplo 2019.

Share :

Facebook Google+ Twitter

Related Posts :